MEL сортировка вершин

День добрый, коллеги!

Самостоятельные поиски пока зашли в тупик, поэтому опишу свое затруднение.

Есть набор выделенных вершин, последовательно соединенных ребрами (ВАЖНО! последовательность ребер может не определяться как loop). Метод выделения не принципиален - ручное выделение вершин или конвертация из выделенных ребер.
В последующей работе нужно отсортировать данные вершины именно в последовательности их соединения, как показанно на рисунке (мне не нужно менять номера вершин, мне просто нужно получить список с вершинами в нужном порядке). Для данного случая речь идет о замкнутой последовательности, поэтому первой можно назначить любую вершину.
Не претендую на готовое решение, буду благодарен, если ткнете носом, где копать.

 

а для чего это нужно?

 

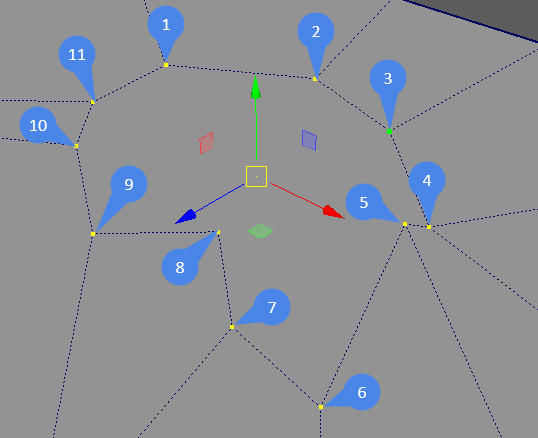
В конкретном примере - для скрипта, формирующего из замкнутой последовательности ребер правильный многоугольник (круг). Вообще не только для этого.

 

Нужно как-то получить координаты пивота выделенных компонентов и от этих данных плясать.

 

Думал над этим. Координаты могут не дать верный результат. Пока в голову приходит только один алгоритм:
Назначаем нулевую точку.
Переводим ее в эджи, получаем все ребра выходящие из этой точки.
Переводим ребра обратно в точки - получаем все вершины, с которыми соединена нулевая.
Сверяем полученные вершины с начальным списком, первую совпадающую, но еще не пронумерованную назначаем вершиной 1.
Повторяем все действия для каждой вершины.
Но этот метод попахивает велосипедом из костылей.

 

У каждого вертекса есть свои эйджи, в данном случае у каждого по 3. Ищем у кого эйдж общий, тот и сосед.

 

Не совсем понял. Что значит "свои эджи". Как я могу получить их список?

 

polyInfo

только непонятно, что это даст, так как нужна точка, относительно которой нужно строить правильный многоугольник

 

Точка, относительно которой строить - это как раз самая маленькая проблема, ее высчитать легко из координат точек. Сложнее с заданием плоскости, в которой должен лежать результат, при условии, что выбранные точки могут не лежать в одной плоскости. Но это я пока оставлю, для начала надо получить работающий скрипт для координатных плоскостей.
З. Ы. Ок, список эджей это хорошо. Хотя тогда надо каждый раз сверять эджи одной вершины с эджами оставшихся... Надо будет разобраться, оптимально ли это. В моем варианте как-то проще отбор выглядит.

 

Типа высчитать центр масс? Просто выделяя компоненты, например "по кругу" в центре появляется пивот этого выделения, только я не нашёл решения как брать координаты этого пивота.

 

даже не задумывался, но можно будет покурить на досуге. Я рассматриваю несколько алгоритмов по нахождению центра - как среднее значение от крайних показателей, как среднее значение от всех точек и как среднее значение с исключением крупных отклонений.
Первый наверное как раз совпадает с пивотом, второй и третий имеют смысл если говорить о неравномерно расставленных точках.

 

Вот вам вариант алгоритма по плучению списка точек по топологии:
1.Так как дырка замкнута, делаем Fill Hole ( polyCloseBorder) Получили новый фейс "Дырка"
2. Если теперь спросить список вершин фейса "Дырка" , то получим их в порядке нумерации, а нам надо в проядки топологии, поэтому далее делаем этому фейсу экструд и получим соответсвенно фейс "Экструд" (можно его уменьшить скейлом для визуального восприятия)
3. Вот теперь если спросить список вершин фейса "Экструд" то получим их тоже в порядке нумерации, но теперь этот порядок будет равен порядку топологии, так как у фейса "Экструд" появились новые вершины, а они были добавлены к вершинам объекта последовательно.
4. Теперь каждой нашей исходной вершине поставлено в соответствие новая вершина на фейсе "Экструд", можно обходить этот фейса по порядку нумерации и брать связанные вершины.
(например так:
4.1 Выбрали одну вершину (на фейсе "Экструд")
4.2 ConvertSelectionToEdges;
4.3 ConvertSelectionToVertices;
4.4 Получили 4 вершины, 3 из них принадлежат фейсу "Экструд", их откинем и получим номер искомой вершины
4.5 берем следующию вершину по порядку из "Экструд" и переходим на пункт 4.2)

5.Бонусом получим центр вершин, как центра фейса "Дырка".

Слов много, но в принципе алгоритм простой.

 

К сожалению, у алгоритма есть большой минус - он не универсален. При отсутсвии как таковой дырки нам надо будет расшивать модель, потом проводить кучу преобразований... Пока мне кажется, что мой вариант алгоритма менее костыльный, т.к. по сути в вашем варианте присутствует тот же набор действий (вершина в эджи, эджи в вершину, перебор лишних), но дополненный еще кучей преобразований.

 

global proc perfectPoly()
{

polyExtrudeFacet -kft true -ls 0.5 0.5 0;

string $selected_face[] = `ls -sl -fl`;


int $number_of_sides = `intSliderGrp -q -v perPoly`;

////////////// POLYMESH ///////////////////////////////////////
string $polymesh[];
tokenize $selected_face[0] ".[]" $polymesh;


////////////// ORDER EDGES ///////////////////////////////////////

string $fte[] = `polyInfo -faceToEdge $selected_face[0]`;

string $order_edges[];
tokenize $fte[0] " :\n\r" $order_edges;
int $size_edgearray = `size $order_edges`;

string $edges[];

for($j=2;$j<$size_edgearray; ++$j)
{
$edges[$j-2] = $polymesh[0] + ".e[" + $order_edges[$j] + "]";
}


////////////// ORDER VERTS ///////////////////////////////////////

string $ftv[] = `polyInfo -faceToVertex $selected_face[0]`;
string $order_verts[];

tokenize $ftv[0] " :\n\r" $order_verts;
int $size = `size $order_verts`;

string $ordered_verts[];
for($i=2;$i<$size;++$i)
{
$ordered_verts[$i-2] = $polymesh[0] + ".vtx[" + $order_verts[$i] + "]";
}

////////////// ARRAY CLEAR ///////////////////////////////////////

clear $fte;
clear $order_edges;
clear $ftv;
clear $order_verts;

////////////// NUMBER OF VERTS ///////////////////////////////////////

int $n = `size $ordered_verts`;

////////////// SORT VERTS/EDGES ///////////////////////////////////////

////////////// SUBDIVIDE EDGES ///////////////////////////////////////

if($n<$number_of_sides)
{
int $remainder = $number_of_sides - $n;
float $g = $remainder/$n;
int $f = `trunc $g`;
int $residue = $remainder - ($f*$n);

select -r $edges[0];
polySubdivideEdge -dv ($f +$residue);

for($k=1;$k<$n;++$k)
{
select -r $edges[$k];
polySubdivideEdge -dv $f;
}
select -r $selected_face[0];
}

////////////// MERGE VERTS ///////////////////////////////////////

if($n>$number_of_sides)
{
int $remainder = $n - $number_of_sides;

if($remainder == 1)
{
select -r $ordered_verts[0];
select -add $ordered_verts[1];
polyMergeVertex -d 10;
}

select -cl;

if($remainder>1)
{
for($j=0;$j<$remainder;++$j)
{
select -add $ordered_verts[$j];
}
polyMergeVertex -d 10;
select -cl;
select -r $ordered_verts[0];
select -add $ordered_verts[1];
polyMergeVertex -d 10;

}
}
select -r $selected_face[0];


////////////// CLEAR ARRAYS ///////////////////////////////////////

clear $selected_face;
clear $edges;
clear $ordered_verts;

////////////////// CONSTRUCT REGULAR POLYGON //////////////////////////////////////////////////////////

string $selected_newverts[] = `ls -sl -fl`;


//Reselect all the verts
string $face_to_verts[] = `polyInfo -faceToVertex $selected_newverts[0]`;
string $order1[];

tokenize $face_to_verts[0] " :\n\r" $order1;
int $size = `size $order1`;

string $ordered_new_verts[];
for($i=2;$i<$size;++$i)
{
$ordered_new_verts[$i-2] = $polymesh[0] + ".vtx[" + $order1[$i] + "]";
}
clear $face_to_verts;
clear $order1;

int $n_gon = `size $ordered_new_verts`;

$theta = (2*3.14159265)/$n_gon;

vector $vert1 = `pointPosition -w $ordered_new_verts[0]`;
vector $vert2 = `pointPosition -w $ordered_new_verts[1]`;
vector $vert3 = `pointPosition -w $ordered_new_verts[$n_gon-1]`;

vector $a = $vert1 - $vert2;
vector $b = $vert3 - $vert2;

vector $cross_ab = cross($b,$a);
float $mag_cross_ab = mag ($cross_ab);

vector $normal = $cross_ab/$mag_cross_ab;

vector $sum = <<0,0,0>>;

for($i=0;$i<$n_gon;++$i)
{
vector $vnow = `pointPosition -w $ordered_new_verts[$i]`;
$sum = $sum + $vnow;
}

vector $centroid = $sum/$n_gon;

vector $v1 = $vert1 - $centroid;

for($i=1;$i<$n_gon;++$i)
{
float $theta_new = $theta*$i;
float $cos_tn = cos ($theta_new);
float $sin_tn = sin ($theta_new);

vector $cross_normV1 = cross($normal,$v1);

vector $v_new = ($v1*$cos_tn) + ($cross_normV1*$sin_tn) + $centroid;

select -r $ordered_new_verts[$i];
move -a ($v_new.x) ($v_new.y) ($v_new.z);

}
select -cl;
select -r $selected_newverts;
clear $ordered_new_verts;
clear $selected_newverts;
clear $polymesh;

}

{
window -title "Regular Polygon" -wh 416 78 Regular_Polygon;
columnLayout;
intSliderGrp -label "Number of Sides"
-fieldMinValue 3 -fieldMaxValue 200
-minValue 3 -maxValue 200 -value 4 -field true perPoly;

button -label "Execute" -c "perfectPoly()";
showWindow;
}

 

Эхх, некогда сейчас полностью курить логику скрипта... Поправьте меня, если я ошибаюсь - данный скрипт делает правильный многоугольник из выбранного полигона? И нумерацию ребер/вершин соответсвенно берет в соотсветствии с нумерацией ребер полигона?
Мне же нужен вариант, когда может быть выбрано произвольное кольцо ребер (например, вертикальный луп на боку корпуса подводной лодки, когда в обе стороны от него куча полигонов).
З.Ы. если не прав, то как вернусь буду более серьезно вникать в данный код.

 

Вот такая дичь получается

 

попробуй выбрать 1 многоугольник, судя по коду должно сработать

 

ну, уже почти работает XD. Все таки я имел в виду именно многоугольник - полигон со множеством вершин. Сам не скоро смогу потестить, к сожалению...

 

Не надо расшивать, если фейс уже есть, тогда сразу начинаем с пункта 2.

Но это все не нужно, симон310 подсказал простой способ

polyInfo -faceToVertex

получим список вершин по топологии от выбранного фейса, то что надо.